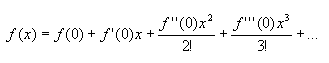
Returns the sine of the radians argument, which we'll call x. This is the most mathematically-intense function, and I have to thank Ian Griffiths again for doing the hard work behind the analysis presented here.
The MacLaurin Series
Altair BASIC's calculation of the sine function is based upon the MacLaurin series. A MacLaurin series is an expansion of functions whose derivatives are continuous.
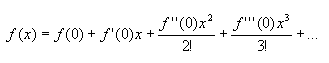
Now, how do we use this series for the sine function? It's going to look like this :
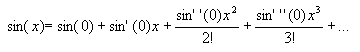
Well, we know that the derivative of sin(x) is cos(x), and the derivative of cos(x) is -sin(x). We also know that sin(0)=0, and cos(x)=1. Therefore the series can be reduced to :
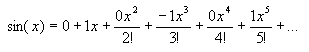
Simplifying a bit further, and limiting the number of terms to a reasonable approximation, we get down to :
![]()
Scaling
To make the code in this and the next section smaller, our first step is to scale our radians argument x into a new variable u that is in the range -1 < u< 1. To do this we first divide x by 2p and then lose the integer part of that number.
| Divide x (in FACCUM) by 2p to get u. | ||||
| 0C95 | CD020A | Sin | CALL FPush | Push x |
| 0C98 | 014983 | LXI B,8349 | BCDE=2p | |
| 0C9B | 11DB0F | LXI D,0FDB | ||
| 0C9E | CD120A | CALL FLoadFromBCDE | rhs = 2p | |
| 0CA1 | C1 | POP B | lhs = x | |
| 0CA2 | D1 | POP D | ||
| 0CA3 | CD3109 | CALL FDiv+2 | u=x/2p | |
| Lose the integer part of u. | ||||
| 0CA6 | CD020A | CALL FPush | ||
| 0CA9 | CDA20A | CALL Int | rhs = INT(u) | |
| 0CAC | C1 | POP B | lhs = u | |
| 0CAD | D1 | POP D | ||
| 0CAE | CD0C08 | CALL FSub+2 | u=u-INT(u) | |
Quadrantization
The second part of the algorithm is an optimisation to reduce u to a 'quadrantized' value, q, so called because it lies within the two quadrants either side of the origin, ie -0.25<q<0.25. Here's a little graph showing sin(x) against u, with the quadrant numbers shown in red.
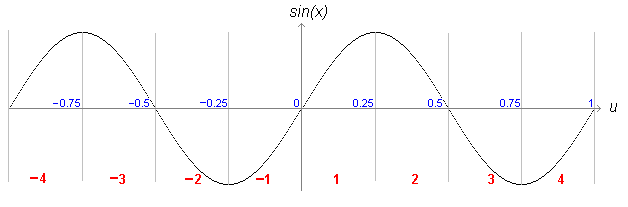
To get from u to q, we don't need to scale again but we do take advantage of two trignometric identities : sin(-x) = -sin(x), and sin(x)=sin(pi-x).
<fixme: insert Monte's explanation here>
So we have our value q. Here's another graph showing sin(x) against the quadrantised value q.
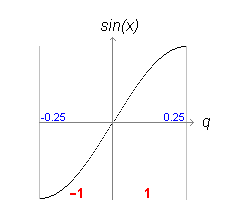
fixme: the comments inlined below are train-of-thought and should not be used. I haven't quite worked this out.
| Firstly we subtract from 0.25 to get x from -0.75<=x<1.25 | ||||
| 0CB1 | 01007F | LXI B,7F00 | BCDE=0.25 | |
| 0CB4 | 51 | MOV D,C | ||
| 0CB5 | 59 | MOV E,C | ||
| 0CB6 | CD0C08 | CALL FSub+2 | ||
| If x is +ve then skip ahead having set the carry flag to indicate we do not need to negate | ||||
| 0CB9 | EF | RST FTestSign | ||
| 0CBA | 37 | STC | Set carry (ie no later negate) | |
| 0CBB | F2C30C | JP NegateIfPositive | ||
|
x is between -0.75 and 0. Here we add 0.5 to get x between -0.25 and 0.25 and signal that negation is required | ||||
| 0CBE | CD0108 | CALL FAddOneHalf | ||
| 0CC1 | EF | RST 5 | ||
| 0CC2 | B7 | ORA A | Resets carry (ie later negate) | |
| Preserve carry flag and negate x if it's +ve. | ||||
| 0CC3 | F5 | NegateIfPositive | PUSH PSW | |
| 0CC4 | F4FA09 | CP FNegate | ||
| Adding 0.25 | ||||
| 0CC7 | 01007F | LXI B,7F00 | BCDE=0.25 | |
| 0CCA | 51 | MOV D,C | ||
| 0CCB | 59 | MOV E,C | ||
| 0CCC | CD1208 | CALL FAdd+2 | ||
| Final negate (depends on above). | ||||
| 0CCF | F1 | POP PSW | ||
| 0CD0 | D4FA09 | CNC FNegate | ||
Progression Calculation
<fixme>
| Push x. | ||||
| 0CD3 | CD020A | CALL FPush | ||
| Push x^2 | ||||
| 0CD6 | CD1D0A | CALL FAccToBCDE | ||
| 0CD9 | CDE508 | CALL FMul+2 | x = x*x | |
| 0CDC | CD020A | CALL FPush | Push x*x | |
| Let q be the first term of the Taylor series. | ||||
| 0CDF | 21030D | LXI H,TAYLOR_SERIES | ||
| 0CE2 | CD0F0A | CALL FLoadFromMem | ||
| Restore x^2 | ||||
| 0CE5 | C1 | POP B | ||
| 0CE6 | D1 | POP D | ||
| 0CE7 | 3E04 | MVI A,04 | ||
| 0CE9 | F5 | TaylorLoop | PUSH PSW | Push #terms remaining |
| Push x^2 | ||||
| 0CEA | D5 | PUSH D | Push BCDE | |
| 0CEB | C5 | PUSH B | ||
| q = (q * x^2) + next term | ||||
| 0CEC | E5 | PUSH H | ||
| 0CED | CDE508 | CALL FMul+2 | ||
| 0CF0 | E1 | POP H | ||
| 0CF1 | CD200A | CALL FLoadBCDE | ||
| 0CF4 | E5 | PUSH H | ||
| 0CF5 | CD1208 | CALL FAdd+2 | ||
| 0CF8 | E1 | POP H | ||
| Restore x^2 to BCDE. | ||||
| 0CF9 | C1 | POP B | ||
| 0CFA | D1 | POP D | ||
| 0CFB | F1 | POP PSW | Pop #terms remaining into A. | |
| 0CFC | 3D | DCR A | Decrement #terms and loop back if not | |
| 0CFD | C2E90C | JNZ TaylorLoop | done all 4 of them. | |
| Finally multiply q by x. | ||||
| 0D00 | C3E308 | JMP FMul | ||
The modified Taylor series used by SIN.
| 0D03 | BAD71E86 | TAYLOR_SERIES | DD 39.710670 | |
| 0D07 | 64269987 | DD -76.574982 | ||
| 0D0B | 58342387 | DD 81.602234 | ||
| 0D0F | E05DA586 | DD -41.341675 | ||
| 0D13 | DA0F4983 | DD 6.283185 |